Belajar persamaan eksponen, sebaiknya disertai dengan rajin berlatih contoh soal. Pada artikel ini akan dibahas 3 contoh soal persamaan eksponen yang menarik untuk dikerjakan.
Secara umum, persamaan eksponen adalah persamaan yang mempunyai variabel di bagian pangkatnya (eksponennya). Adapun pembagian jenis persamaan eksponen ada 3, yakni persamaan eksponen berbasis konstanta, lalu persamaan eksponen berbasis fungsi, dan persamaan eksponen dalam bentuk operasi penjumlahan.
Pada contoh soal persamaan eksponen berikut, kamu diperlihatkan 3 soal yang mewakili tiga jenis kategori tersebut. Dengan begitu, kamu bisa mempelajari ketiga jenis persamaan eksponen pada kesempatan ini.
Baiklah, untuk yang ingin segera mengerjakan soal, maka kamu bisa gulir ke bawah dan melihat soalnya. Pembahasan tiap soal tercantum di akhir artikel. Tetapi, jangan nyontek saat mengerjakan soal ini ya. Kerjakan dulu soal-soal berikut tanpa melihat kunci jawaban. Selamat mengerjakan!
Contoh Soal Persamaan Eksponen

1. Tentukan penyelesaian dari persamaan berikut:
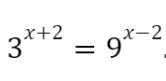
2. Tentukan himpunan penyelesaian dari persamaan eksponen berikut:
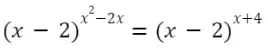
3. Tentukan penyelesaian dari persamaan eksponen berikut:
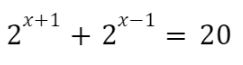
Penyelesaian Contoh Soal Persamaan Eksponen
Nomor 1
Seperti yang dijelaskan di soal, kamu diminta untuk mencari penyelesaian dari persamaan berikut. Berdasarkan sifat-sifat eksponen, maka kamu harus menyamakan basis kedua ruas persamaan tersebut terlebih dulu. Caranya sebagai berikut:
3^x+2 = 9^x-2
Maka, ubahlah 9 menjadi 3^2.
3^x+2 = (3^2)^x-2
Dikarenakan kedua ruas sudah sama, maka selanjutnya kamu bisa ikuti langkah berikut.
x + 2 = 2(x – 2)
x + 2 = 2x – 4
Selanjutnya:
x – 2x = -4 – 2
-x = -6
Dikalikan -1 maka: x = 6
Jadi, penyelesaian dari persamaan tersebut adalah x = 6. Agar lebih jelas, kamu bisa melihat gambar di bawah.
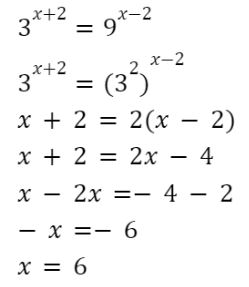
Nomor 2
Soal nomor 2 memerlukan penyelesaian yang cukup panjang, yakni melalui 4 tahap. Berikut lebih jelasnya.
Penyelesaian Pertama
x^2 – 2x = x +4
Pindahkan x + 4 ke ruas kiri agar menjadi:
x^2 -2x – x – 4 = 0
x^2 – 3x – 4 = 0
Setelah itu, lakukan pemfaktoran berikut:
(x – 4)(x + 1)
Maka, kamu memperoleh:
x = 4 atau x = -1
Penyelesaian Kedua
x – 2 = 1
x = 1 + 2 = 3
Jadi, x = 3
Penyelesaian Ketiga
x – 2 = -1
x = -1 + 2 = 1
Jadi, x = 1
Selanjutnya, periksa jika x = 1, apakah g(x) dan h(x) sama-sama genap atau sama-sama ganjil? Maka kamu perlu melakukan uji pangkat untuk ruas kiri dan ruas kanan.
x^2 – 2x = 1^2 – 2(1) = – 1 (hasil dari uji ruas kiri = ganjil)
x + 4 = 1 + 4 = 5 (hasil dari uji ruas kanan = ganjil)
Dikarenakan sama-sama ganjil, maka x = 1 adalah solusi yang tepat.
Penyelesaian Keempat
x – 2 = 0
x = 2
Selanjutnya, lakukan hal yang sama dengan penyelesaian ketiga. Uji apakah untuk x = 2, maka g(x) dan h(x) sama-sama bernilai positif atau tidak.
x + 4 = 2 + 4 = 6 (hasil dari uji ruas kanan = bilangan positif)
x^2 – 2x = 2^2 – 2(2) = 0 (hasil dari uji ruas kiri = bukan bilangan positif)
Oleh karena, hasil dari uji ruas kiri = 0 (bukan bilangan positif), maka x = 2 bukanlah solusi yang tepat.
Jadi, himpunan solusi / penyelesaian dari persamaan eksponen di atas adalah {-1, 1, 3, 4}.
Nomor 3
Untuk mencari penyelesaian persamaan pada soal nomor 3, maka kamu bisa lakukan cara berikut.
2^x+1 + 2^x-1 = 20
2^x . 2 + (2^x) / 2 = 20
Selanjutnya, kalikan dengan 2:
2 . (2^x . 2) + 2 . 2^x / 2 = 2 . 20
2^x . 4 + 2^x = 40
4 . 2^x + 2^x = 40
Misalkan 2^x = y, maka kamu memperoleh:
4y + y = 40
5y = 40
y = 8
Selanjutnya, ubah y menjadi 2^x lagi sehingga:
y = 2^x
2^x = 8
Maka, x = 3 karena 2^3 = 8.
Jadi, penyelesaian dari persamaan eksponen di atas adalah x = 3. Agar lebih jelas, kamu bisa mengklik gambar berikut.

Itulah beberapa contoh soal persamaan eksponensial. Bila kamu tertarik untuk mengerjakan soal lainnya, maka kamu bisa mengklik contoh soal aritmatika, contoh soal tekanan hidrostatis dan contoh soal SPLTV.



