Permutasi, biasanya materi ini diberikan setelah kamu berkenalan dengan aturan perkalian dan faktorial dalam Bab Peluang. Apa itu Permutasi? Bagaimana contoh penerapannya dalam kehidupan sehari-hari? Pada artikel ini kamu akan mengenal dan mempelajari banyak hal tentang Permutasi, mulai dari pengertian, jenis hingga contoh soal permutasi.
Baiklah, kencangkan sabuk pengamanmu karena perjalanan menjajaki dunia permutasi akan segera dimulai. Meluncuuur!
Pengertian Permutasi

Apa itu permutasi? Secara sederhana, permutasi dapat diartikan sebagai cara menyusun obyek dengan memperhatikan urutan. Perlu digarisbawahi, urutan menjadi salah satu hal yang penting dalam permutasi.
Hal ini agak berbeda dari kombinasi yang merupakan cara menyusun obyek tanpa memperhatikan urutan. Agar lebih jelas, kamu bisa menyimak perbincangan antara Baki dan temannya berikut ini.
Contoh permutasi dan kombinasi dalam percakapan
Pada suatu hari yang cerah, Baki bertemu dengan sahabatnya di sebuah rumah makan. Usai menyantap makan siang, mereka berbincang dengan serunya. Percakapan mereka kurang lebihnya seperti ini:
Baki: Bro, I need your help. Gue butuh 5 orang nih buat bentuk group band. Kalau bisa hari Senin udah dapet ya.
Teman Baki : Oh, okey coba ya gue bantu. Kriterianya kayak gimana?
Baki: Udaah bebas, yang penting bisa main alat musik.
Teman Baki: Sip gue catet. Sebentar ya gue post nih di socmed.
Beberapa menit kemudian,
Teman Baki: Eh udah ada yang contact gue nih. Namanya Irma katanya bisa main suling.
Baki: Oke, bagus. Bagi nomornya bro.
Teman Baki: 087835777944, jangan salah ketik ya.
Baki: Siap, thanks ya!
Teman Baki: Syiip!
Bisa temukan mana kasus permutasi dan kombinasi dalam percakapan di atas?
Nah, dari percakapan di atas kamu sudah mendapatkan dua contoh kasus, yakni kasus permutasi dan kombinasi. Bisa tebak yang bagian mana yang menunjukkan permutasi dan bagian mana yang merujuk pada kombinasi?
Pada saat Baki meminta temannya untuk mencarikan 5 orang untuk membentuk grup band, maka itu adalah kombinasi. Kok gitu? Iya, sebab urutan tidak menjadi perhatian utama disini. Sementara, perbedaan yang mencolok dapat kamu jumpai pada saat Baki meminta nomor Irma (kandidat anggota grup band). Kemudian, teman Baki menjawab:
“087835777944, jangan salah ketik ya.”
Dari sini kamu dapat memahami bahwa jika Baki tidak mencatat nomor yang dibagikan oleh temannya secara benar dan urut, maka Baki bisa salah sambung. Bukannya terhubung dengan Irma, Baki mungkin justru terhubung dengan orang lain.
Dengan kata lain, Baki harus mencatat nomor Irma dengan benar – persis seperti yang diinfokan oleh temannya tersebut, yakni 087835777944.
Jika Baki mengabaikan urutan pada saat mencatat nomor tersebut, maka Baki tidak dapat menghubungi Irma. Sampai disini, apakah sudah jelas?
Nah, kamu sudah memahami bahwa kombinasi tidak menaruh perhatian pada urutan, sementara permutasi sangat memperhatikan urutan. Selanjutnya, mari kenali jenis-jenis permutasi.
Jenis Permutasi
Berbincang mengenai permutasi (P) itu sendiri, tahukah kamu bahwa konsep ini terbagi ke dalam beberapa macam?
Secara garis besar, permutasi dikelompokkan menjadi 3 jenis, yakni permutasi dengan unsur yang sama, permutasi dengan n unsur berbeda dan permutasi siklis (melingkar). Lebih jelasnya, simak pembahasan berikut ya.
Permutasi dengan unsur yang sama

Permutasi dengan unsur yang sama merupakan permutasi yang memuat beberapa unsur penyusun / elemen / anggota yang sama. Contohnya pada kata BUKU, terdapat unsur penyusun yang sama, yakni huruf U.
Pada prinsipnya, permutasi ini patut memperhatikan secara detail bahwa tidak diperbolehkan adanya kemungkinan yang sama atau diulang.
Rumus
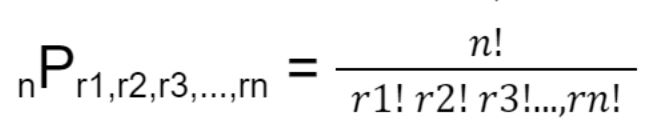
Dengan ketentuan sebagai berikut.
P = Permutasi
n = jumlah total kejadian yang tersedia
r = jumlah unsur penyusun yang sama
Contoh Soal Permutasi dengan Beberapa Unsur Sama
Terdapat sebuah tempat pensil yang berisi 6 buah pensil. Dari 6 pensil tersebut, ada 3 pensil gambar (lukis), 2 pensil warna dan 1 pensil menulis. Jika Baki menyusun seluruh pensil tersebut secara teratur dalam sebaris, maka berapakah banyak susunan yang bisa dibuat?
Pembahasan
Seperti yang tertera di soal, jumlah total pensil ada 6 buah, maka n = 6. Lalu, ada 3 pensil lukis (r1 = 3), 2 pensil warna (r2 = 2) dan 1 pensil menulis (r3 = 1), maka banyaknya susunan yang mungkin adalah:
6P(r1, r2, r3) = 6! / 3! 2! 1!
6P(r1, r2, r3) = 6 x 5 x 4 x 3! / 3! 2! 1!
Maka,
6P(r1, r2, r3) = 6 x 5 x 4 / 2 x 1 x 1 x 1 = 120 / 2 = 60
Jadi, ada 60 cara untuk menyusun 6 buah pensil tersebut.
Untuk memperoleh gambaran lebih jelas maka kamu dapat membaca Pengertian dan Contoh Soal Permutasi Unsur Sama.
Permutasi dengan n unsur berbeda

Permutasi dengan unsur yang berbeda merupakan permutasi yang memuat unsur / obyek berbeda. Misalnya, kamu diminta memilih ketua dan wakil ketua organisasi dari 5 kandidat yang mendaftar. Maka, kamu akan mendapati bahwasanya kelima kandidat tersebut merupakan orang yang berbeda dan orang yang dipilih untuk mengisi 2 jabatan pun merupakan individu yang berbeda.
Rumus

Dengan ketentuan berikut.
P = permutasi
n = jumlah kejadian yang tersedia
r = jumlah kejadian yang harus dipilih
! = sumber faktorial
Contoh Soal Permutasi dengan Unsur yang Berbeda
Sebuah komunitas yang memiliki anggota sebanyak 8 orang ingin membuat susunan pengurus harian yang terdiri dari ketua, wakil ketua, sekretaris dan bendahara. Maka berapakah banyak susunan pengurus harian yang mungkin?
Pembahasan
Seperti yang telah dijelaskan, bahwa seluruh anggota ada 8 orang, sementara yang dipilih hanya 4 orang, yakni untuk mengisi jabatan ketua, wakil ketua, sekretaris dan bendahara. Maka:
n = 8
r = 4
8P4 = 8! / (8 – 4)!
8P4 = 8! / 4!
Sehingga:
8P4 = 8 x 7 x 6 x 5 x 4! / 4!
8P4 = 8 x 7 x 6 x 5 = 1.680
Jadi, ada 1.680 cara untuk membuat susunan 4 pengurus harian komunitas tersebut.
Agar lebih memahami tipe permutasi ini maka kamu bisa mengakses Pengertian dan Contoh Soal Permutasi Unsur Berbeda.
Permutasi Siklis (Melingkar)

Permutasi siklis atau melingkar merupakan permutasi yang digunakan untuk menyusun unsur / obyek berbeda dalam kondisi melingkar. Ada beberapa contoh dari permutasi siklis, misalnya menentukan tempat duduk sekelompok orang yang duduk melingkar, menentukan posisi dalam permainan kucing dan tikus, posisi manik-manik pada kalung atau gelang dan sebagainya.
Rumus
Pn = (n – 1)!
Dengan ketentuan sebagai berikut.
P = Permutasi
n = jumlah total kejadian yang tersedia
Contoh Soal Permutasi Siklis
Sebuah kelompok diskusi terdiri dari 5 orang, mereka harus duduk dalam sebuah meja yang sama. Jika harus menentukan tempat duduk para anggota, maka berapakah variasi yang dari tempat duduk yang mungkin?
Pembahasan
Seperti yang tertera di soal, bahwa jumlah keseluruhan anggota kelompok diskusi adalah 5 orang. Sementara, mereka harus duduk bersama dalam meja yang sama. Maka:
n = 5
P = (n-1)!
P = (5-1)! = 4!
Sehingga:
P = 4 x 3 x 2 x 1
P = 24
Jadi, ada 24 variasi tempat duduk yang mungkin bagi kelompok diskusi yang beranggotakan 5 orang tersebut.
Lebih jelas mengenai permutasi ini, maka kamu bisa mengakses Pengertian dan Contoh Soal Permutasi Siklis.
Aplikasi Permutasi dalam Kehidupan Sehari-hari
Kamu sudah mengenal 3 jenis permutasi, tahukah kamu apa fungsi dari permutasi? Banyak, kamu dapat menggunakan permutasi untuk berbagai aktivitas keseharian, misalnya menyusun peralatan dalam wadah dengan susunan yang berbeda. Apa lagi ya contoh aplikasi permutasi dalam kehidupan sehari-hari? Berikut diantaranya:
- Menyusun plotingan job desk saat kerja secara berkelompok
- Menentukan variasi tempat duduk dalam posisi melingkar
- Menyusun daftar piket
- Memilih pengurus kelas, komunitas hingga organisasi
- Membuat variasi pakaian
- Menyusun variasi menu makanan
- Mengambil pemenang / juara (1, 2, 3 dan seterusnya) secara berurutan
- Menyusun nomor telepon, nomor kupon, nomor antrian, angka, warna dan sebagainya.
Itulah beberapa contoh aplikasi permutasi yang bisa kamu jumpai sehari-hari. Agar lebih memahami materi permutasi, kamu bisa mengerjakan contoh soal berikut. Inilah contoh soal permutasi dan pembahasannya yang bisa kamu jadikan bahan belajar.
Contoh Soal Permutasi dan Pembahasannya
Selamat ya, kamu sudah mengetahui beberapa jenis permutasi. Tetapi, agar lebih memahami permutasi, maka kamu bisa mengerjakan beberapa contoh soal berikut ini. Pertanyaan-pertanyaan ini dilengkapi dengan pembahasan, jadi kamu bisa berlatih sambil belajar. Siap memulai? Here you go!
Contoh Soal Permutasi #1
Pada sebuah kotak berukuran sedang terdapat 3 buah bola yang masing-masing berwarna hijau, merah, dan kuning. Jika Baki diminta untuk mengambil 2 buah bola secara acak, sementara urutan pengambilannya harus diperhatikan, maka berapakah banyak permutasi yang bisa digunakan untuk mengambil 2 buah bola dari kotak tersebut?
Penyelesaian
Karena permutasi sangat memperhatikan urutan, maka:
nPr = 3P2 = 3! / (3-2)! = 3! = 3 x 2 x 1 = 6
Ada 6 cara mengambil 2 buah bola dari dalam kotak tersebut. Secara detail, kemungkinannya adalah:
Hijau-Merah, Hijau-Kuning, Merah – Hijau, Merah-Kuning, Kuning-Hijau, dan Kuning-Merah.
Contoh Soal Permutasi #2
Terdapat 3 sahabat bernama Baki, Cia dan Dina. Jike mereka harus menempati 3 kursi yang tersedia di ruang kelas maka berapakah banyak variasi tempat duduk yang bisa dilakukan ketiga sahabat tersebut menggunakan konsep permutasi?
Penyelesaian
Seperti yang tertera di soal, terdapat 3 sahabat (Baki, Cia, dan Dina) yang harus menempati 3 tempat duduk yang tersedia. Jika menggunakan rumus permutasi, maka:
nPr = n! / (n – r)!
3P3 = 3! / (3 – 3)!
3P3 = 3! / 0! = 3 x 2 x 1 = 6
Jadi, ada 6 variasi tempat duduk yang mungkin bagi Baki, Cia dan Dina. Secara manual, kamu bisa menuliskan:
Baki – Cia – Dina
Baki – Dina – Cia
Cia – Baki – Dina
Cia – Dina – Baki
Dina – Cia – Baki
Dina – Baki – Cia
Contoh Soal Permutasi #3
Jika harus terdiri dari 4 angka, maka ada berapa banyak bilangan yang dapat kamu susun menggunakan 2275?
Penyelesaian
Untuk menyelesaikan soal ini, maka kamu bisa menggunakan permutasi dengan unsur yang sama. Seperti apa rumusnya? Coba baca lagi, maka kamu pun ingat bahwa rumus permutasi dengan unsur yang sama adalah sebagai berikut:
nPr = n! / (n-r)!
Nah, setelah menuliskan rumusnya, selanjutnya kamu bisa memasukan nilai. Seperti yang tertera di soal, jumlah angka yang tersedia ada 4, yakni 2, 2, 7 dan 5. Sementara, unsur penyusun yang kembar (angka 2) ada 2 buah, sehingga r = 2.
4P2 = 4! / (4 – 2)!
4P2 = 4! / 2! = 4 x 3 x 2 x 1 / 2 x 1 = 24 / 2 = 12
Jadi, ada 12 variasi bilangan yang bisa terbentuk dari angka 2275.
Itulah pengertian dan jenis permutasi lengkap dengan contoh soal permutasi. Setelah menyimak pembahasan ini, apakah kamu semakin tertarik untuk belajar Permutasi?
Pada dasarnya, permutasi tidak sulit untuk dipelajari, namun membutuhkan ketelitian. Oleh karena itu, sebaiknya kamu rajin berlatih soal agar kamu terbiasa menghadapi masalah-masalah yang berkaitan dengan permutasi. Dengan demikian, kamu juga lebih lihai menyelesaikan masalah permutasi.
Melalui cara ini, kamu juga dapat memahami konsep masing-masing tipe permutasi serta mampu menerapkannya ke dalam masalah yang sesuai. Oiya, jangan lupa bersyukur atas progress belajar yang telah kamu capai ya. Ingat, kamu sudah belajar banyak hari ini.



