Wah, pada artikel sebelumnya kamu sudah mempelajari permutasi dengan unsur yang sama, sekarang giliran kamu mempelajari permutasi dengan n unsur berbeda.
Tak hanya menyelami teori, namun kamu juga akan diajak untuk mengerjakan contoh soalnya. Seperti apa contoh soal permutasi unsur berbeda? Sabar, baca penjelasan berikut ini dulu ya!
Pengertian dan Rumus Permutasi Unsur yang Berbeda

Permutasi unsur yang berbeda adalah permutasi yang terjadi pada saat kamu memilih sebagian atau semua dari sejumlah obyek berbeda yang tersedia. Misalnya, ketika kamu harus menyusun 3 buku (dari total 3 buku) berbeda dalam satu baris. Atau, kamu harus menyusun 3 balon dari total 8 balon yang tersedia. Banyaknya cara untuk menyusun benda-benda tersebut bisa diketahui melalui permutasi unsur yang berbeda.
Rumus Permutasi dengan Unsur Berbeda
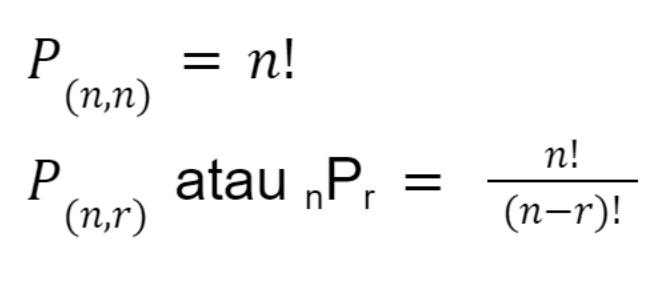
Dengan keterangan sebagai berikut:
n = total unsur
r = sebagian unsur yang ditanyakan
Kedua rumus tersebut memiliki penggunaan yang berbeda. Biar lebih paham, mari terapkan rumus ini pada contoh soal permutasi unsur berbeda berikut.
Contoh Soal Permutasi Unsur yang Berbeda dan Pembahasannya
Contoh Soal Permutasi Unsur Berbeda #1
Jika suatu klub catur yang beranggotakan 8 orang ingin membuat susunan pengurus harian yang terdiri dari 4 jabatan, yakni Ketua, Wakil Ketua, Sekretaris dan Bendahara, maka berapakah banyaknya peluang susunan panitia yang mungkin?
Penyelesaian
Seperti yang tertera di soal, bahwa jumlah anggota ada 8 maka n = 8. Banyaknya orang yang dipilih adalah 4 karena jabatan yang tersedia ada 4 maka r = 4, sehingga:
8P4 = 8! / (8 – 4)!
8P4 = 8! / 4!
Bila dijabarkan maka:
8P4 = 8 x 7 x 6 x 5 x 4! / 4!
Coret 4! pada pembilang dan penyebut karena keduanya habis dibagi masing-masing, sehingga:
8P4 = 8 x 7 x 6 x 5 = 1.680
Jadi, ada 1.680 cara untuk membentuk susunan 4 pengurus harian dari 8 anggota klub.
Contoh Soal Permutasi Unsur Berbeda #2
Terdapat komunitas Healthy People yang hendak memilih ketua, sekretaris dan bendahara. Jika jumlah anggota komunitas ada 20 orang, maka berapakah banyaknya cara menyusun pengurus komunitas tersebut?
Penyelesaian
Untuk menyelesaikan soal ini kamu dapat menggunakan rumus permutasi:
nPr = n! / (n-r)!
Tetapi, sebelumnya tentukan dulu n dan r-nya. Seperti yang telah dijelaskan di soal, kamu dapat menyimpulkan bahwa n = 20 dan r = 3. Selanjutnya, ikuti langkah berikut.
20P3 = 20! / (20 – 3)!
20P3 = 20! / 17!
Maka,
20P3 = 20 x 19 x 18 x 17! / 17!
20P3 = 20 x 19 x 18 = 6.840
Jadi, ada 6.840 cara untuk menyusun ketua, sekretaris dan bendahara pada komunitas Healthy People yang beranggotakan 20 orang.
Contoh Soal Permutasi Unsur Berbeda #3
Sekolah SMA HargaBelanja.com setiap tahun mengadakan acara pensi. Biasanya, delapan bulan sebelum acara, para siswa melakukan pemilihan untuk jabatan ketua dan wakil panitia. Setelah melakukan seleksi, ada 5 murid yang lolos ke tahap selanjuntnya, yakni Asya (A), Bimo (B), Cika ( C), Dion (D) dan Evan (E). Dengan informasi tersebut maka berapakah banyak cara memilih ketua dan wakil untuk acara pensi tersebut?
Penyelesaian
Seperti yang telah dijelaskan dalam soal bahwa banyaknya kandidat adalah 5, sementara jabatan yang tersedia ada 2. Jadi, kamu bisa menyimpulkan bahwa n = 5 dan r = 2.
5P2 = 5! / (5 – 2)!
5P2 = 5! / 3!
Maka,
5P2 = 5 x 4 x 3! / 3!
Setelah dihitung secara teliti, hasilnya:
5P2 = 20
Jadi, ada 20 cara untuk menyusun ketua dan wakil panitia dari 5 kandidat tersebut.
Contoh Soal Permutasi Unsur Berbeda #4
Seorang resepsionis klinik Hargabelanja.com ingin mencetak nomor antrian pasien. Nomor antrian tersebut terdiri dari 3 angka dari 1, 2, 3 dan 4 tanpa memuat angka yang sama. Maka, berapakah banyak pilihan nomor antrian jika:
a) nomor antrian tersusun dari 3 angka pertama
b) nomor antrian menggunakan 3 dari total 4 angka yang tersedia
Penyelesaian
Berikut cara menyelesaikan contoh soal permutasi dengan unsur berbeda ini.
a) Jika resepsionis memakai 3 angka pertama, yakni 1, 2 dan 3 maka nomor antrian yang dapat terbentuk adalah:
P33= 3!=321=6
Jadi, ada 6 angka kupon antrian.
b) Sementara itu, jika resepsionis memilih 3 angka dari total 4 angka yang tersedia, maka susunan nomor antrian yang dapat terbentuk adalah:
4P3 = 4! / (4 – 3)!
4P3 = 4! / 1! = 4 x 3 x 2 x 1 = 24
Jadi, terdapat 24 pilihan susunan nomor antrian yang dapat terbentuk.
Itulah beberapa contoh soal permutasi unsur berbeda dan pembahasannya. Sebelumnya kamu juga sudah menyimak pengertian tipe permutasi ini dan rumusnya. Bagaimana, apakah sekarang kamu tidak bingung lagi?
Jika menemukan soal seperti ini lagi, maka kamu bisa gunakan cara penyelesaian yang sama. Buka kembali artikel ini kalau kamu lupa atau membutuhkan bahan belajar. Selanjutnya, mari tengok pengertian dan contoh soal permutasi siklis.




Komentar ditutup.